12月6日，新一期地平线「你好，开发者」工具链技术专场在智猩猩顺利完结直播。专场由地平线模型转换和量化工具负责人何道远主讲，主题为《地平线模型转换和训练后量化部署》。

本文是此次专场主讲环节的实录整理。如果对直播回放以及Q&A有需求，可以点击阅读原文前去观看。

要将量化后的PTQ模型部署到硬件上，还需要将它转换成全整型计算模型，才能把量化性能发挥出来。

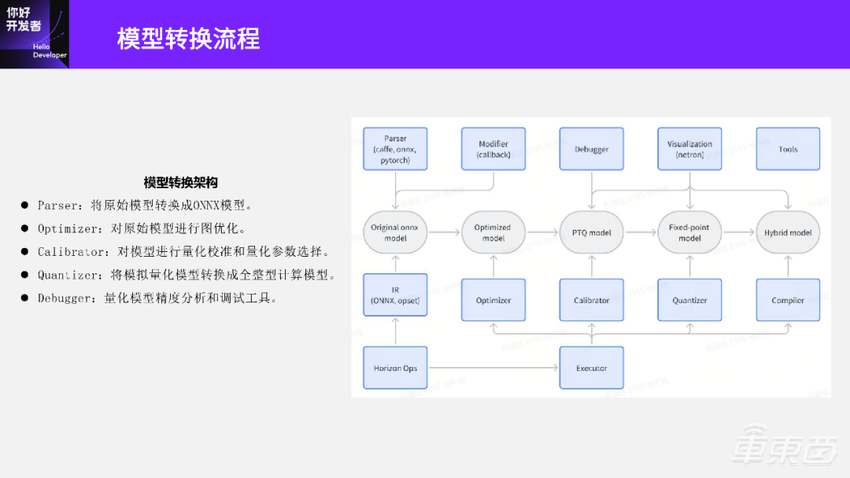
用户的模型可以是Caffe、PyTorch或者ONNX等，进来之后会先经过一个Parser，得到一个Original onnx model；接着将 Original onnx model送到下一个Optimizer模块里去，Optimizer模块会对原始输入的模型进行图优化，图优化之后会得到一个优化后的Optimized模型；接着再将Optimized模型送到下一个Calibrator模块，对浮点模型进行量化校准和量化参数选择，然后生成一个PTQ model；再将PTQ model送到下一个Quantizer模块，负责将PTQ模型转换成一个全整型计算的定点模型；最后将定点模型送到Compiler里面，生成一个可部署的Hybrid model。架构图里面还有一个Debugger模块，是我们今天也会讲到的，这个模块负责对量化模型进行精度分析和调试。

我们再讲一下模型计算图优化这部分，先看一下右边两张图：

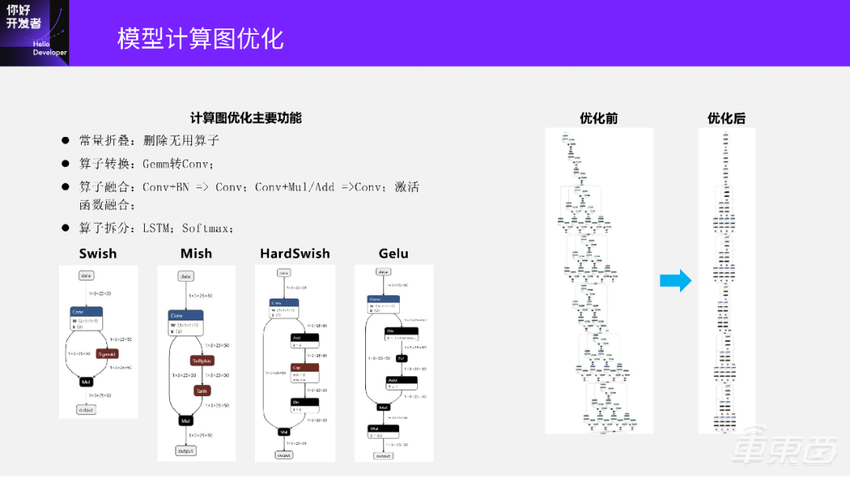
前面这张是模型优化前的结构图，后面是图优化之后的模型结构。优化后的模型结构相比优化前的已经少了很多算子，也更简洁，基本是一串算子从头到尾。当我们去部署这两个模型的时候，优化后的模型会比优化前模型的执行效率高。

我们再看一下图优化模块里面包含哪些内容呢？

1、常量折叠
首先会包含常量折叠，就是将一些原始的模型中的常量数据在离线端算出来。这样做的好处是，不需要在推理的时候再计算这些节点了，可以节省模型推理的时间。另外，原始模型中可能还包含一些无用算子，比如Dropout，因为推理的时候就不再需要Dropout这种算子了，也可以在模型转换阶段先把这类算子删除掉。如果这个模型包含多个输出分支，且进行模型部署的时候存在无用分支，那么可以在模型转换阶段删除掉，这样也可以节省模型推理的耗时。

2、算子转换
算子转换部分需要尽可能将Gemm算子转换成Conv算子，这样在后面对模型进行量化的时候，就只需考虑Conv算子的量化，不需要考虑Gemm算子的量化逻辑了。

3、算子融合
算子融合常见的有：Conv+BN可以融合成一个Conv算子；Conv加Mul或者Add，大部分情况下可以融合成一个Conv算子，这样在部署的时候可以提高性能。

另外，还有激活函数的融合。它的主要问题是ONNX算子没有高级别的激活函数的表示，比如下面4个图：

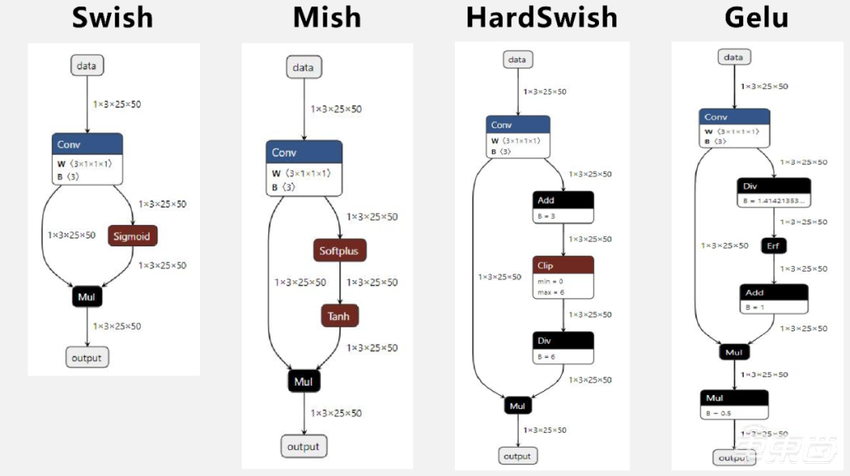
Swish算子在ONNX里面是Sigmoid+Mul；Mish是Softplus+Tanh+Mul三个算子；HardSwish是4个算子；Gelu是5个算子组成。

如果不融合这些激活函数会有两个问题：

一个是部署Gelu的时候需要推理计算5个算子。如果将这些算子融合成一个Gelu算子，就可以提升推理效率。

另一个是如果不融合这些算子，量化也会是个问题。比如Swish是由Sigmoid和Mul两个算子组成的，如果不进行融合就需要对Sigmoid和Mul都进行量化，量化的精度损失会更大一些。如果是Gelu就更夸张，需要对5个算子都进行量化，这样模型精度会有显著的损失。

所以，我们工具链中的做法就是先把这些激活函数都进行融合成一个单独的算子，然后再进行量化和部署。我们会在后面的量化内容里讲到，地平线的工具链是怎么对各种激活函数进行统一的量化和整型化。

4、算子拆分
除了算子融合以外，有些地方还需要对算子进行拆分，典型有Softmax和LSTM。

我们先看一下LSTM，左边这张图就是对LSTM算子拆分。

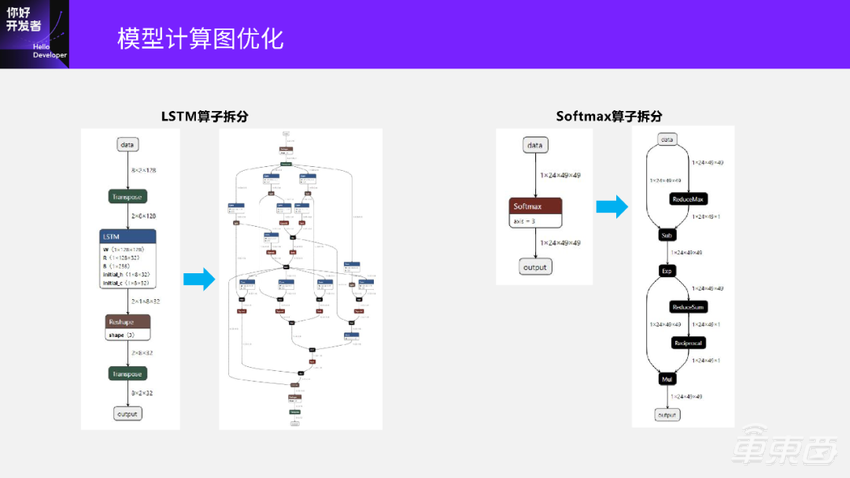
如果用这个包含LSTM算子的原始模型去部署，会发现硬件上并没有一个计算单元对应到LSTM，导致LSTM这个模型是不能部署的。我们知道LSTM就是由Conv+Sigmoid+Tanh+Mul这些基本算子组成的，这些算子在硬件上都是被支持的。所以，一个做法是可以将LSTM进行拆分，旁边这个图是将LSTM拆分之后的网络结构。拆出来之后，这个计算图里面就没有完整的LSTM了，只有一些细粒度的算子。这些细粒度的算子都是可以被硬件支持的，所以这个结构的模型就可以尝试部署到硬件上了。

再看右边这张图，是一个Softmax算子。

同样，硬件上没有一个计算单元来对应到Softmax算子。但我们可以尝试将Softmax拆分成最右边这张图，包含6个基本算子。这些基本算子都是可以被硬件支持的，拆分完之后的计算图就可以尝试部署到硬件上了。

我们后面会讲到，如果要对这样的计算图真正进行部署，还需要进行量化和定点化。这里面的Conv算子量化部署是比较常见的，主要难的是这些非线性激活函数Sigmoid、Tanh、Exp的量化部署问题。

当模型进行图优化之后，下一步就需要将其从浮点模型转换成量化模型。

主要包含三个步骤：

第一步，将浮点模型转换成模拟量化模型；
第二步，在模拟量化模型上面进行量化参数搜索，得到最优的量化参数；
第三步，将优化之后的模拟量化模型转换成一个全整型量化模型。

我们先看浮点模型到模拟量化模型的转换。

浮点模型转换成模拟量化模型就是在浮点模型的一些位置上插入伪量化节点，由伪量化节点模拟硬件的量化行为。看一下这幅图里左边的第一幅这个是原始全精度模型，插入一些伪量化节点之后就变成第二个图称为模拟量化模型（或者伪量化模型）。

第二个图里面这些绿色的节点一般叫做伪量化节点，可以来模拟硬件是如何对数据进行量化的。

那么，如何将第一个全精度模型变成第二个模拟量化模型？是在每个输入的地方都插入一个伪量化节点吗？

实际上不是这样的，这里还要看算子的属性。首先要看这个算子是不是可量化的，一般情况Conv都是可量化的，所以在Conv的输入、输出上都插入一个量化节点，来模拟Conv在硬件上的量化行为。

那什么是不可量化算子？简单的讲只要量化之后会导致模型精度显著下降的算子，都是不可量化算子。

那怎么识别这样的算子呢？我们后面在量化模型误差分析里面会讲到，可以通过Layerwise的方法识别这些算子的量化敏感度。如果识别到一个Conv是量化敏感节点，它的量化会导致模型精度显著下降，那么就可以把这个Conv标记为不可量化节点，这样我们就不会在 Conv的输入上插伪量化节点了。

还有一对概念是主动量化和被动量化。

主动量化算子是那些在模拟量化算子转成定点算子的时候，需要用到该节点输入、输出上的量化参数的这类算子。比如，我们后面会讲到将Conv节点转换成定点QConv节点时需要用到输入和输出的Q/DQ节点中的量化参数。如果这个算子在量化成整数计算的定点算子的时候，并不需要用到输入、输出上的量化参数，那么就是被动量化算子。

我们只需要在主动量化算子上面去插入伪量化节点，被动量化算子是不需要插入的。

刚才提到的Conv是主动量化算子，那什么是被动量化算子呢？看一下第四个计算图。MaxPooling前面也有一个伪量化算子，但不是给MaxPooling用的，而是给前面的Conv输出用的。MaxPooling的计算并不会改变输入、输出的数值，只需要从输入里面选出最大的数值，将MaxPooling进行整数化的时候不需要感知输入上的量化参数。所以MaxPooling输入、输出是不需要伪量化算子的。

回到第二个图的激活节点上，激活节点前后都有一个伪量化节点。如果这个激活是Relu，而Relu是不需要感知数据量化参数的，那么前后的两个伪量化节点是可以删掉一个的（留下的一个是用来量化Conv输出的）；但如果激活不是Relu，而是前面提到的Swish、Gelu这些，那么前后两个伪量化节点都是需要保留的。

讲完模拟量化模型，我们再来看一下模拟量化模型的（Q/DQ）伪量化节点的具体行为。

伪量化节点的作用是将输入的浮点FP32数据先做一次量化，再做一次反量化，还是以FP32输出，使整个模型保持浮点计算，但是可以用来模拟硬件的量化行为。伪量化节点的主要行为是刚才提到的量化函数图片和反量化函数图片两个式子。这两个式子里面包含主要的计算逻辑是：先对输入的x除以scale，再取一次round，加上一个zero_point做偏移，最后再做一次clip就得到量化后数据。

量化节点有哪些参数可以选呢？主要有三类：

一类是量化方法。

刚才提到的zero_point是0就是对称量化，非0是非对称量化；round括号里面 x除以scale，scale如果在整个数据的量化过程中是一个固定的值，那么它就是一个均匀量化；如果scale不是一个固定的值，那就是一个非均匀量化；如果scale是在模型推理的时候计算的就是动态量化；如果它在模型转换过程中离线计算的，就是静态量化。

第二类是量化精度。

每个量化节点可以选择不同的量化精度，比如4bit、8bit、16bit等。

第三类参数是量化粒度。

量化粒度看上面这个式子图片，round里面图片这一项，如果x代表的是某一层的整个激活，也就是整个激活用的是同一个scale量化，那就是per-tensor量化；如果对某一个激活的每个通道选择不同的scale，那就是per-channel量化。同理，我们还可以对scale选择粒度更小一点，就有了per-block以及其他量化方法。

介绍完模型转换部分，再看一下模型量化误差分析。

02 模型量化误差分析

量化可以提升模型部署效率，但是做过模型量化的同学一般都遇到过量化后模型精度下降的问题。想要分析模型量化精度损失原因，调试精度问题，并找到根本原因尝试修复精度损失，通常是比较耗时且困难的工作。

我们首先看一下量化误差的来源。

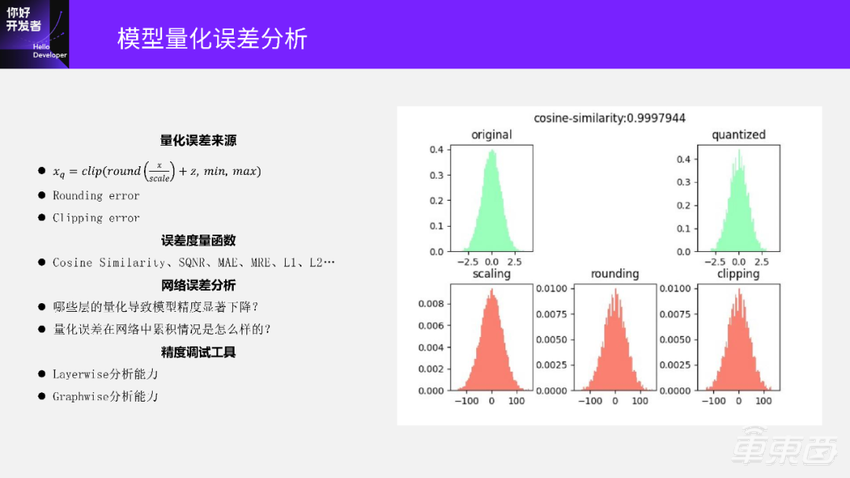
对于量化误差的来源还是先看量化公式图片，量化公式实际上有三个部分：

首先对输入的浮点x数据除以scale；再做一次Round操作，这是一个取整操作；再做一次Clip操作，让数据饱并到我们想量化的数值范围里面。

看一下右边这两个图：

左上角这个绿色的图是原始的浮点数据分布。首先对原始数据做一次scale得到第二排第一个红色分布的图；再做一次Round得到了中间这张红色分布图；然后做一次Clip得到右下角这张图；最后再把数据再反量化回去， 得到了右上角量化后的数据分布图。可以看到相比原始的数据分布，量化后的数据分布已经有明显的差异了，这种差异是最终导致模型精度下降的原因。

再来看一下中间几个步骤，可以看到rounding这个分布图，相比左边scaling这个分布图，已经产生了明显的误差，这个误差我们叫做rounding error。rounding error主要和两个部分有关：一个是round策略，另一个是 scale大小，scale代表量化步长。如果scale越小，量化步长越小，round之后误差也会越小；如果scale选的越大，round之后误差也会更大。

Clipping操作产生的误差主要是在数据分布的两端，图上靠近-100和100的地方。仔细看这附近会发现这里和前面rounding分布图是有一些差异的，Clipping的误差它主要来源于两个部分：

一个是Clipping的时候选择min、max的大小，它的大小和想要量化的数据表示有关：如果量化成INT8，那么min、max分别是-128和127；如果量化成INT16，那么这个min、max分别是-32768和32767。

另外，clipping error也和scale有关，如果scale选择越小，那么x除以scale这一项就会越大，取整之后的值也越大，容易超出min、max范围，从而被截断掉产生clipping error；如果scale选择比较大，x除以scale这一项比较小，就不容易超min、max范围，从而clipping error就会减小。

了解了量化误差的来源，我们怎么去度量量化误差呢？

从上面这两个绿色分布图来看，原始数据分布图和量化之后的数据分布图是有一些误差的，怎么度量误差的大小呢？一般常用的度量函数有Cosine Similarity（余弦相似度）、SQNR、MAE、MRE、L1、L2等，这里我们选用余弦相似度来度量量化误差。余弦相似度的好处是一个归一化的数值，量化之后两个分布的余弦相似度接近1.0，表示量化误差比较小。如果这两个分布的余弦相似度比较小，就代表量化之后的误差比较大。

明白了量化误差来源，同时也有了量化误差的度量函数之后，我们怎么分析模型网络的误差呢？

这里面主要考虑两个问题：一个是哪些层的量化会导致模型精度的显著下降？另一个是量化误差在网络中累积情况是怎样的？

要回答这两个问题就回到第一页PPT架构图里面讲的Debugger工具，我们需要开发一个精度调试工具来分析这两个问题。精度调试工具主要包含两个功能：一个是Layerwise分析能力，另一个是Graphwise分析能力。

Layerwise分析是用来回答第一个问题的，模型中哪些层的量化是导致模型精度下降的主要原因？我们先看一下 Layerwise分析是怎么计算的，下面这张图左边是浮点模型，右边是量化模型。

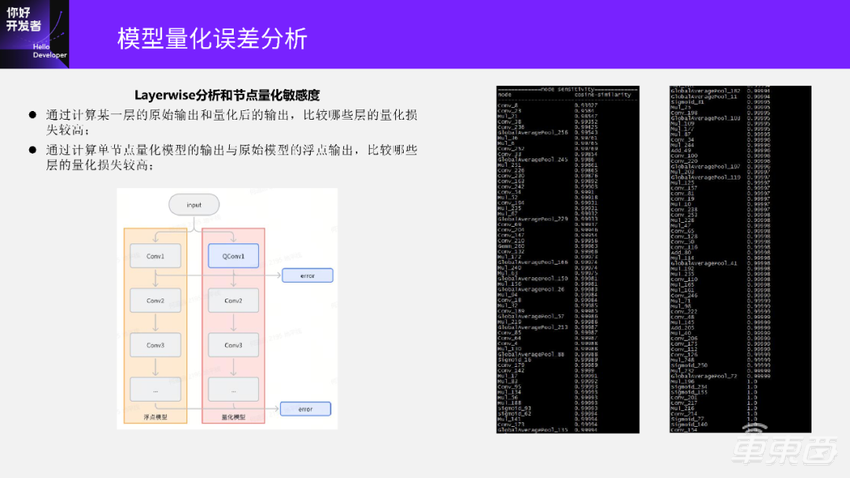
Layerwise分析的计算是在相同输入下计算量化QConv和原始Conv输出的误差，计算所有层的误差并收集起来进行比较，可以看到哪些层量化误差会比较大。当然表示每一层的误差可以是单层的输出误差，也可以用这个模型的最终输出误差。

收集完这些误差之后，可以看到右边这两张图：

这是一个模型里面所有层的误差。因为这个模型比较大，就把它截成了两张图。这里的误差已经进行了排序。可以看到这张图的前半部分，这些层的余弦相似度是比较低的，代表着这些层的量化误差会比较大；后半部分余弦相似度比较高，代表着这些层的量化误差比较小。得到了Layerwise量化节点误差的分析之后，下一步一个比较简单的办法是把这些量化误差比较大的层设置成不量化，就可以恢复模型精度了。

接下来我们再看一下Graphwise分析方法，先看Graphwise的计算逻辑。

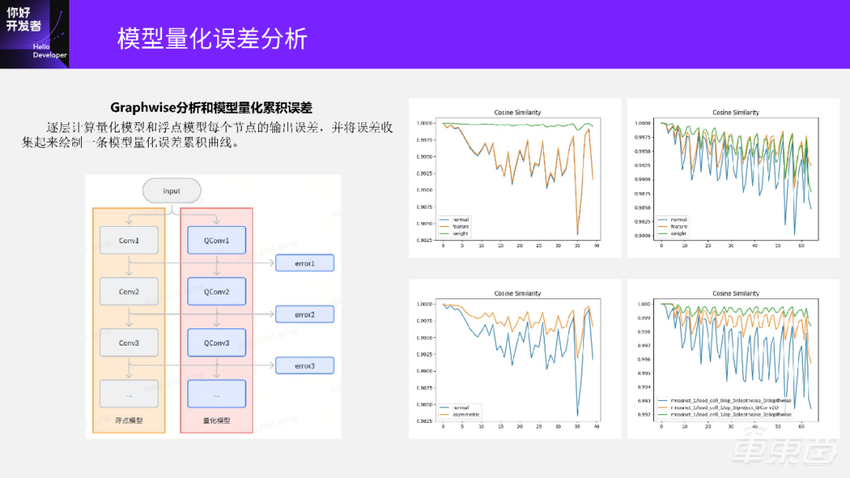
同样左边是浮点模型，右边是量化后的模型。Graphwise的分析就是把每个QConv输出和原始Conv输出的误差逐层的计算出来，把这些误差绘制成一条曲线，用来分析这个模型的量化误差累积情况。

先看左上角这张图，横坐标是节点索引，纵坐标是误差，这里误差还是用余弦相似度来评估。绿色曲线代表对模型只量化权重，可以看到这条线基本是靠近1.0的，表示量化模型误差损失比较小；橙色曲线代表的是这个模型只量化激活，这条曲线余弦相似度比较低，且波动比较大。这两条曲线就意味着这个模型的权重量化损失比较小，但激活量的损失会比较大。

再看右边这张图，它是相反的。前半部分这条绿色的权重量化曲线更靠近1.0，余弦相似度比较高；但到了模型的尾部部分，绿色这条量化曲线降得比较多，甚至比橙色的曲线的余弦相似度掉的更多了。这张图表示的意思是模型的权重量化误差比激活量化误差还要更大一些。

另外，我们还可以在没有数据集的情况下评估，用不同的量化方法得到的量化模型的好坏。比如左下角这张图，蓝色normal曲线表示对模型对称量化，橙色的曲线表示非对称量化。可以看到非对称量化的累积误差曲线的余弦相似度更高一些，代表这个模型的非对称量化结果比对称量化的结果更好一点。

最后是右下角这张图，它是对模型进行部分量化，这里有三条曲线，绿色这条曲线的余弦相似度更靠近1.0，代表三种不同部分量化选择下，选用绿色这条曲线对应的这一组节点得到的部分量化模型精度最好。

前面介绍完量化模型的量化精度损失问题，接下来我们看一下怎么通过不同的量化方法减少模型精度损失并恢复量化模型的精度。

03 模型训练后量化（PTQ）

首先，我们看一下有哪些量化方法。

我们根据模型量化过程中是否需要数据、label以及梯度等，把不同的量化方法按照易用性做了分级：纵坐标代表量化方法或量化工具的使用复杂度或使用成本；横坐标是对这些量化方法进行了分级。

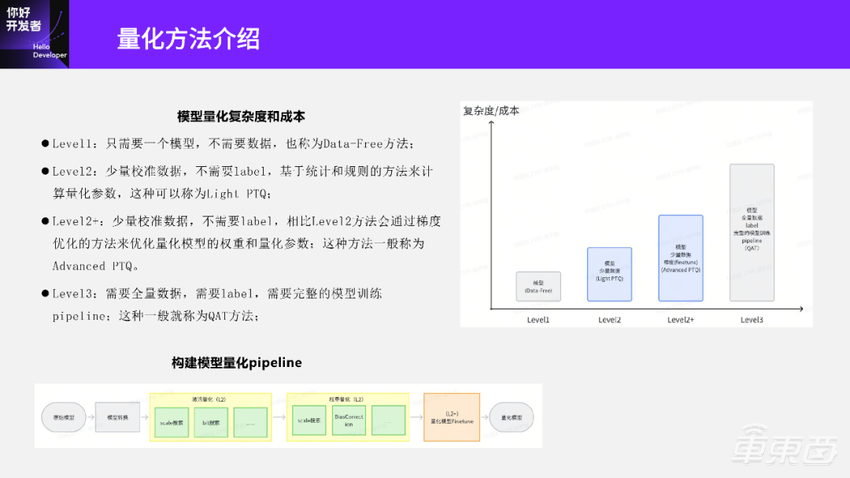
最左边的level1量化方法只需要一个模型，其他都不需要，我们叫做Data-Free的量化方法。

level2方法需要一个模型以及少量的数据，然后基于统计和规则的方法来计算量化参数，这种方法可以称为Light PTQ。

Level2+方法在模型和少量数据的基础上，可以基于梯度下降的方法优化模型的量化参数。这种方法一般叫做Advanced PTQ。

Level3方法需要模型、全量数据和label，需要完整的模型训练Pipeline。这就是我们之前分享过的QAT量化方法。

一般情况下，模型量化精度损失比较小，可以用 level2的Light PTQ方法。如果这个模型量化精度损失比较高，那就可能需要尝试用Level2+ Advanced PTQ方法甚至Level3 QAT方法去恢复量化模型精度。对于PTQ量化，主要考虑level2和level2+里面的方法。这两个范围里的方法，细分下去又有很多不同的方法。怎么来应用这些方法呢？我们就需要构建一个量化Pipeline来处理这些方法。

整个模型量化Pipeline大概是左下角这张图。原始模型进来，先通过一个模型转换优化，得到一个优化后的模型；优化后的模型送到 PTQ模块里做量化，而PTQ模块又分成三个部分：

第一步是激活的量化。对这些激活上的 Q/DQ伪量化节点进行量化参数选择，包括scale、bit等参数；第二步，我们再把它送到权重量化模块里面。同样地，权重量化模块也会对权重节点上的伪量化节点的量化参数进行选择。权重量化里面还有BiasCorrection等的方法；第三步，我们把这个模型再送到一个包含Level2+量化方法的Finetune模块里面。

最后，我们就得到了一个经过PTQ量化的模型，这个模型和前面提到的伪量化模型的区别是，这个PTQ模型里面所有的Q/DQ节点的量化参数都已经固定了。

接下来先看一下激活量化这部分。

首先还是看一下量化公式，公式里面的所有参数都是可以通过搜索来选择或优化的包括 scale、round、min、max、clip。前面我们也讲到，对量化误差影响比较大的是scale。它会影响rounding error，也会影响clipping error。scale是怎么计算的呢？就是右边的公式。这里我们把zero_point这项去掉，先只看对称量化。

可以看到这个 scale受两个参数影响，一个是Threshold，另一个是Bit。

Threshold是怎么计算的呢？可以看下面这个图。

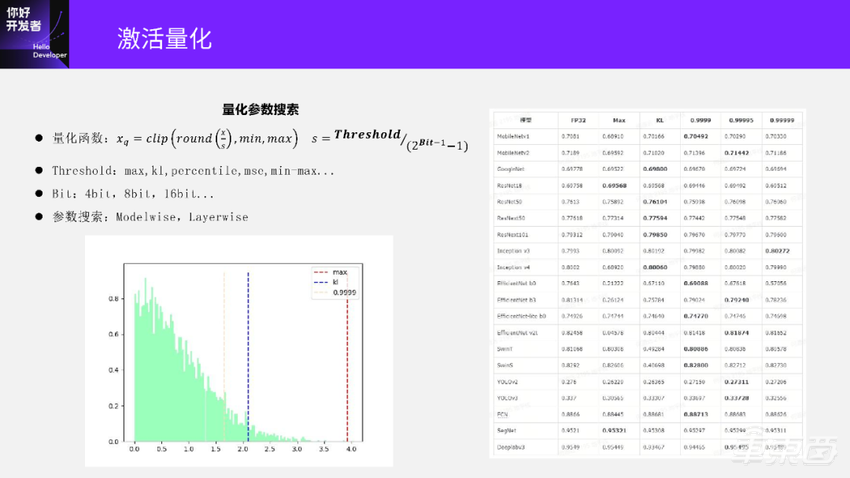
Threshold是在数据分布里面找到一个最优的截断值，最优的截断值可以让数据的量化误差损失最小。常用的Threshold的计算方法有max、kl、percentile、mse、min-max等，min-max已经属于非对称量化的方法。

max表示在这个数据分布里面取绝对值最大的值作为阈值Threshold。

percentile是一个百分数，它表示对这个数据分布的所有数从大到小排序。如果percentile取0.9999，那表示要取这个数据分布里面第99.99%大的那个值。

kl的计算会尝试在这个数据分布里面取多个阈值，对每个阈值进行数据的量化；取量化后和原始数据kl散度最低的阈值，作为量化损失最小的最优阈值。但实际上，KL散度最低对应的阈值并不一定是在整个模型中的量化误差最小、最合理的。

有了这些阈值方法之后，我们怎么来计算模型中各个激活的量化参数呢？

1、Modelwise

刚才讲到每种阈值方法选择的Threshold也并不一样。简单一点，我们可以用Modelwise的方法来计算。Modelwise就是整个模型尝试用不同的Threshold方法去计算，得到多个不同的量化模型，再来比较这些量化模型的好坏，选出最优的量化模型。

右边这个图就是不同模型选用不同的阈值方法去量化的结果，标粗的是这个模型最优的量化结果。

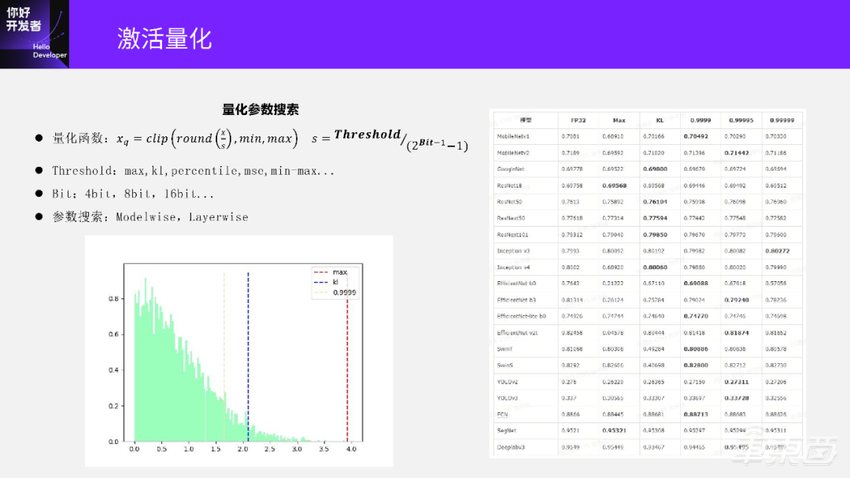
可以看到，有几个模型是 Max方法最好、精度最高，也有的是KL和 Percentile方法，而Percentile方法也不都是同样一个百分数是最优的。另外，我们还可以观察到里面有几个模型 Max方法的精度下降特别厉害，这是因为 Max校准总是取数据分布里面的最大值作为阈值。大家可以看到，如果Threshold取的是最大值，那么 scale也相对会比较大，相应的Rounding error就会比较大。当这个模型的数据分布中存在比较大的离群值时，就会导致scale算得特别大，Rounding error也特别大，最终导致模型精度显著下降。所以， Max方法虽然在有些情况下是最优的，但用它来量化模型时，波动比较大。

还有一个问题，我们通过Modelwise得到几个量化模型后，怎么知道哪个量化后的模型是最优的？右边这张图是我已经用数据把这些模型精度跑出来了，实际作为一个模型转换和后量化工具，如果真的要用全量数据去评测，时间成本上是不可接受的。

评价这些不同量化方法得到的模型的好坏，可以用前面在量化误差分析里面提到Graphwise的分析方法，对这些不同方法得到的量化模型绘制量化误差曲线，去比较哪一条曲线的余弦相似度更接近1.0，从而得到最优的量化模型。

2、Layerwise

除了Modelwise方法以外，我们还可以更细粒度的做Layerwise的量化参数选择。

Layerwise可以对每一层激活尝试用不同的阈值，比较这些不同的阈值得到的量化误差，选出误差最小的作为这一层最优的量化参数并固定下来。

Layerwise还可以融合Bit搜索。对量化敏感度比较低的、量化后误差比较小的层，可以尝试选用更低的量化Bit比如4Bit。对一些量化敏感度比较高、量化之后误差比较大的层，可以选用比较高的Bit，比如用16Bit去量化，这样就得到一个部署上最优的模型。

接下来我们再看一下权重的量化部分。

权重的量化也可以和激活量化一样，通过搜索的方式得到最优 scale和Bit等量化参数。此外，权重量化还有一些其他方法来优化模型。

先讲一下BiasCorrection这个方法。它的核心思想是：量化的时候会产生误差，这些误差往往是有方向性的，导致模型的输出发生偏移，最终导致模型精度的下降。如何修正这些偏移呢？修正这些偏移就是用到BiasCorrection方法。

下面这个图是BiasCorrection的方法，和之前计算误差的图比较像也是左边是浮点模型，右边是量化模型。

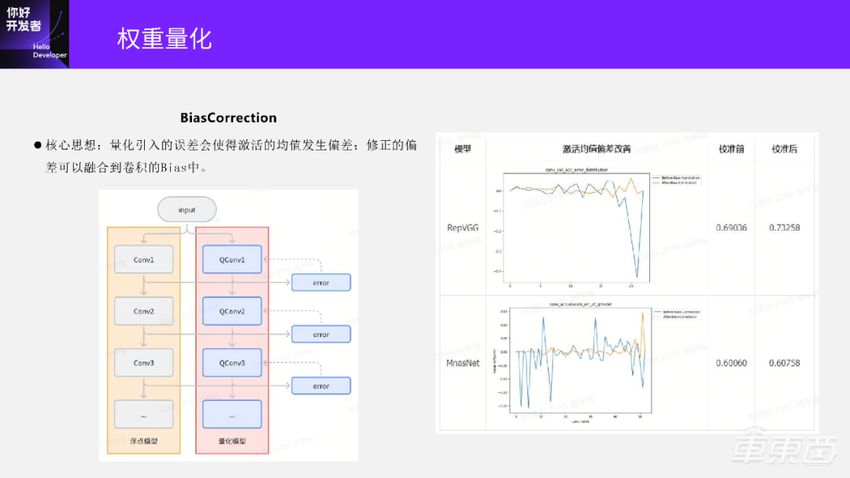
这里计算每一层量化Conv和原始Conv的输出，并计算两者在每个通道上的平均误差，把平均误差看作量化产生的偏移。因为平均误差是每个通道上计算的，所以和 Bias是相同形状的，我们就可以把计算得到的平均误差融合到卷积的Bias里面去，这就完成了偏差的校准。这里融合的另一个好处是不会在模型部署的时候带来额外的性能影响。

我们再可以看一下右边的两个实例模型：

上面是 RepVGG模型。蓝色曲线是BiasCorrection校准之前的偏差曲线，橙色是校准之后的偏差曲线，可以看到校准前后还是有明显变化的。对应到量化模型精度在校准前精度只有0.69，校准之后可以到0.732，还是有显著的提升的。

下面是MnasNet模型。前半部分它的校准偏差还是得到了显著地抑制，但在模型输出部分，校准偏差并没有得到很好地抑制，甚至还出现了反方向的偏差。对应到最终的模型精度上还是有一点点提升，但实际上提升已经不明显了。

我们再看一种权重量化的方法，除了BiasCorrection校准以外，我们也可以对权重进行校准。权重校准的方法常用的有跨层均衡量化和SmoothQuant方法。

在这里我们介绍一种地平线早期做的激活权重均衡量化方法，这个方法和后来SmoothQuant方法有点像。它的主要思想是激活的每个通道分布差异可能会比较大，比如右下角这两个图，是从ConvNext模型里面取出来的两层激活分布的箱线图。

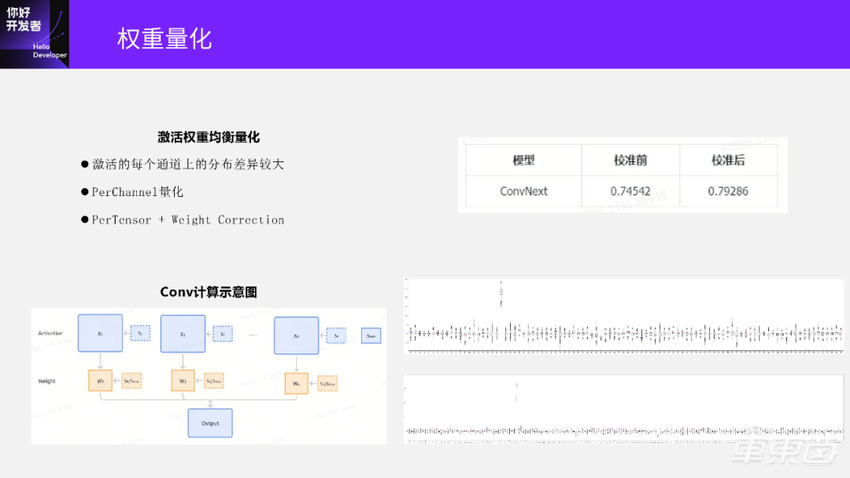
横坐标表示激活通道，纵坐标表示激活的幅值。上面这张图中间有一个通道上的激活幅值远远大于其他通道上，下面这张图也有一个通道上的幅值远大于其他通道。为什么ConvNext会出现出现这种通道间的幅值差异特别大的情况呢？主要是因为ConvNext这个模型和传统的 CNN模型不一样，传统的 CNN模型中我们归一化层用的是Batchnorm，而ConvNext中归一化层用的是Layernorm。Layernorm的归一化方法和Batchnorm不一样，容易出现不同通道之间的数据分布差异比较大的情况。

我们对通道之间幅值差异比较大的激活尝试量化的时候，scale的选择就会比较困难。如果这个scale选的比较大，那么对幅值异常通道上的量化就会比较友好，但这会导致其他幅值比较小的通道上的量化rounding error比较大。但如果scale选的比较小，其他通道上比较好，但是幅值比较大的通道上的 Clipping error 就会比较大。这就是用PerTensor量化面临的问题，怎么解决呢？

一个简单的方法就是用PerChannel量化，给每个通道都选一个scale，使每个通道的scale都是独立的、互不影响的。这样每个通道都可以用一个比较合理的scale去保证比较小量化误差。但激活引入PerChannel量化会导致一些硬件上的计算代价，甚至硬件上需要增加一些额外的计算单元来支撑这个功能。所以我们希望激活还是PerTensor量化，这里就用到了一个激活权重均衡量化的方法。

我们看一下左下角的Conv计算示意图：上面每个蓝色框代表一个通道的激活，每个橙色的框代表着一个通道的权重。而Conv的计算就是用通道上的权重去卷积激活，再把所有通道上得到的结果进行累加。每个通道上的卷积计算可以表示成 X*W，如果要在卷积计算上乘一个系数，这个系数是乘在X还是 W上，都是一样的。

假设现在已经对激活进行per-channel量化，每个通道上得到了一个scale分别是S0，S1，Sn，我们可以从per-channel的scale里面提取一个最大的scale记作Smax。提取出来之后，每个通道原本的scale需要除以Smax，比如第一个通道的scale除以Smax变成了S0/Smax，第二个通道就变成S1/Smax。

激活跟scale之间是乘法关系，刚才讲到了在卷积计算的过程中，如果要乘以一个系数，这个系数是乘在激活上还是权重上都是一样的。所以我们可以把变换后的每个通道的激活scale参数融合到权重里面，这样激活就只保留一个所有通道公共的Smax参数，相当于转换成了per-tensor量化。而每个通道的权重则分别被一个scale进行了校准。这个方法相当于是用Weight校准之后的权重+PerTensor激活量化来代替per-channel的激活量化。

回到ConvNext模型上，在没有应用激活权重均衡量化方法之前，模型精度是0.74，应用了这个方法之后精度可以提升到0.792。

前面讲的都是基于搜索和规则的方法来计算和优化量化参数，我们也可以通过梯度下降的方法来优化模型的量化参数。这种方法可以优化量化公式里的所有参数，右边这个图蓝色框里的参数都是可以优化的，包括 scale、Bit，甚至 Round策略以及Weight等。

基于梯度下降的模型Finetune优化策略主要有右边这三种：End-to-End，Layerwise，Blockwise。

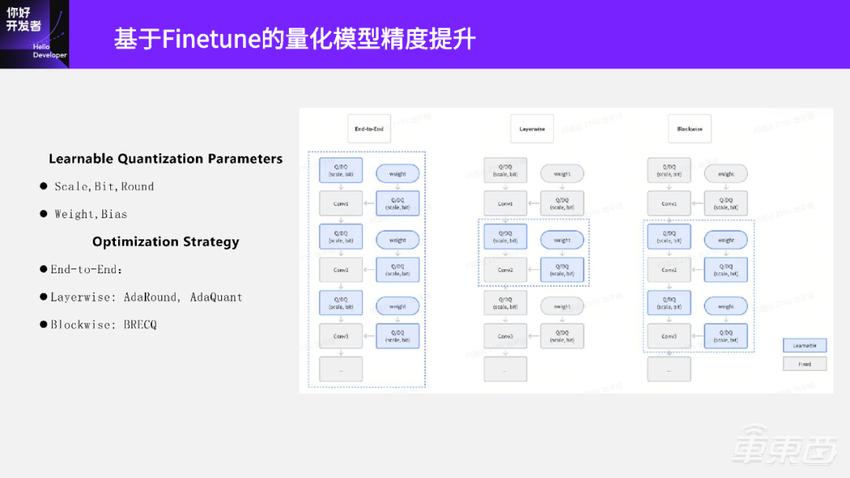
1、End-to-End

End-to-End是对整个模型的量化参数一起优化。一般做法是拿量化模型和原始模型的输出MSE误差作为 loss来优化这些量化参数。这种方法的一个比较大的问题是：如果在一个较小的数据集上去优化，会有较大的过拟合风险，但是一般情况下也不会同时去优化所有的量化参数。

2、Layerwise

Layerwise是每次只优化调整某一层的量化参数。比如中间这个图当前这一步只优化Conv2的量化参数，用量化后的Conv2输出与原始Conv2输出的MSE作为loss，去优化 Conv2节点的量化参数，典型的做法有AdaRound、AdaQuant。

AdaRound每次优化时只优化权重，且在优化调整权重的时候把调整幅度限制在0或1上。这样，AdaRound最后优化的结果就相当于给权重量化选了一个最优的Round策略。

AdaQuant是AdaRound方法演变过来的，不再只局限于调整Weight，所有参数都可以调整，包括激活的scale、Bit，以及权重，甚至这一层的Bias。在权重的优化上也不再限制调整范围，幅度可以是任意的。这种方法的好处是，因为每次只调整一个节点的量化参数，所以可以在一个比较小的数据集上训练优化，不会产生比较大的过拟合风险。

3、Blockwise

有了End-to-End和Layerwise，自然就有了介于这两种方法之间的第三种方法Blockwise，典型的有BRECQ方法。Blockwise方法是每次去优化一个Block，Block一般是手动指定几个层，每次只调整指定的几个层里量化参数，所以 该方法中指定Block大小是其中一个关键问题。

不过，大家如果做的是Transformer模型上的优化，那每次调整的Block大小可以固定是一个Transformer Block就可以了。

04 模型全整型量化

前面我们讲的是如何生成一个模拟量化模型，介绍的 PTQ方法也都是在模拟量化模型上去做量化参数的搜索和优化。真正要将量化 后的PTQ模型部署到硬件上，还需要将它转换成全整型计算模型。

大家可以看到这里有三个图，左边是全精度的模型，就是FP32的模型；中间是模拟量化模型，也叫做伪量化模型；右边是全整型模型，叫做定点模型。

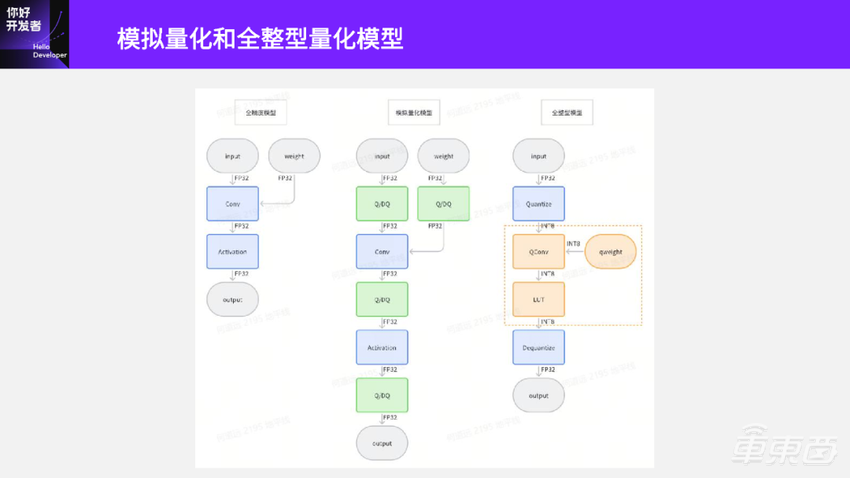
模拟量化模型比全精度的模型多了一些Q/DQ伪量化节点。如果将模拟量化模型拿去部署，就会发现性能是没有提升的，反而是下降的。因为模拟量化模型 Conv输入还是FP32，和原始浮点模型Conv计算量是一样的，反而还多了很多Q/DQ伪量化节点，所以性能肯定是下降的。

想要将量化后模型的性能发挥出来，还需要将量化后的模型进行全整型量化，也就是定点化。定点化之后可以得到右边这个图，这时候Conv节点已经变成了QConv节点，它的输入、权重、输出都是INT8。这个QConv节点相比原来浮点模型里面的Conv节点，计算量就有显著下降了。此外，原始浮点模型里面的Activation节点输入和输出都是FP32；到了全整型模型里面已经转换成一个LUT（查表算子）节点，输入和输出也变成了INT8。

全整型量化模型的头尾还有两个节点Quantize和Dequantize节点。这两个节点还是浮点的，若要想优化这两个节点，需要在模型部署阶段进行优化了。一般做法是把Quantize节点和数据前处理去进行融合，把Dequantize节点和数据后处理融合，这样就可以最大化地发挥部署模型的性能。

我们再看一下浮点的Conv到定点的Conv是如何转换的？

1、

先看一下最上面Conv的计算公式。我们在第三部分模型训练后量化（PTQ）里讲到，通过PTQ量化得到了Conv的输入、输出以及权重的量化参数，就是scale。

2、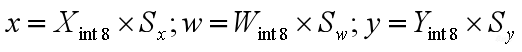

有了每一个数据上的量化参数，用反量化公式来表示。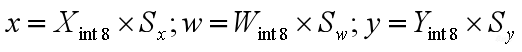

3、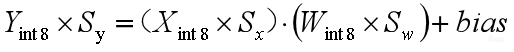
再把这些量化公式带到上面的浮点计算公式里面，就有了第三个公式。这就是Conv的量化计算公式。

4、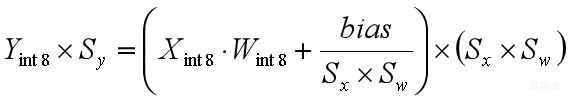

对量化计算公式做一些等效变换，把（Sx*Sw）提出来，括号里面就得到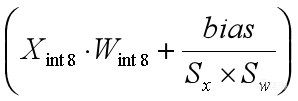，在括号外面是（Sx*Sw）。可以看到（Xint8×Wint8）这一项已经是整数计算了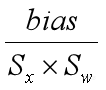，这项还是浮点的，下一步我们就把这一项也转成定点。

5、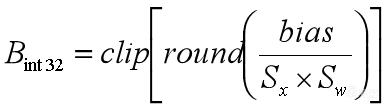

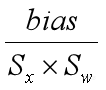这一项转变比较容易。我们把它直接取一次round，就变成整型了，再做一次clip是保证数据不要溢出量化范围。

6、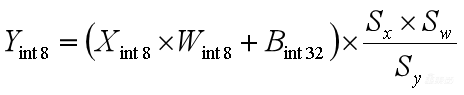

一般情况下我们会把量化到int32范围。对它进行量化之后，我们再把Sy移过来，就得到了最后的量化公式，这就已经是Conv的量化计算公式了。

大家如果是在GPU上做模型量化部署的话，到这一步就可以了。因为GPU是有浮点计算能力的，只要保证中间卷积部分是定点计算的，部署模型的推理就是高效，后面的量化部分可以用浮点算（这部分计算量占比不大）。但是如果我们的目标是全整型计算，最后这项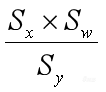还是浮点的，还需要把这一项也转成定点的。这一项在量化里面一般叫做Requantize。

我们先把这项表示为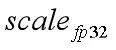。再把它拆成。浮点数在二进制上的表示本来就是指数项和小数项，只不过这里拆的时候要保证范围在0.5~1之间的，这样可以保证mantissa在量化的时候误差损失最小。得到之后，这一项是个常数。在硬件上做右移就行了，是个整数操作，这里唯一还有mantissa是0.5~1的小数。

那怎么样把mantissa转化成整数呢？我们在mantissa上去乘一个较大的值，比如在mantissa上乘2^15取一下，就变成了一个整数了。乘上怎么消除呢？就把它提到前面去，在指数exponent上加上15，就变成第三这个式子。

这里有两个约等于主要是因为mantissa乘整项取round时候会有误差损失，可以根据硬件代价做权衡。如果想要保留尽可能高的精度，那就用更大的整数去乘mantissa，比如mantissa×2^31，这样乘完之后做round就保会保留更多的有效位数。

如果要权衡硬件代价，选择更小的也可以，可以比15更小，12、13都是可以的。

我们可以把requantize这项记作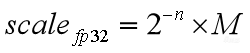，把这个式子代回到量化公式里面，就得到了右边这个式子。括号里面都是整数计算，M也是一个整数，而2^-n在硬件上就是一个右移的操作，也是整数计算。

到这一步，我们就完成了浮点Conv到全整型Conv计算的转换。

然后我们再看一下全整型Conv计算在硬件上是怎么做的。下面这个图就是Conv在硬件上计算的示意图。

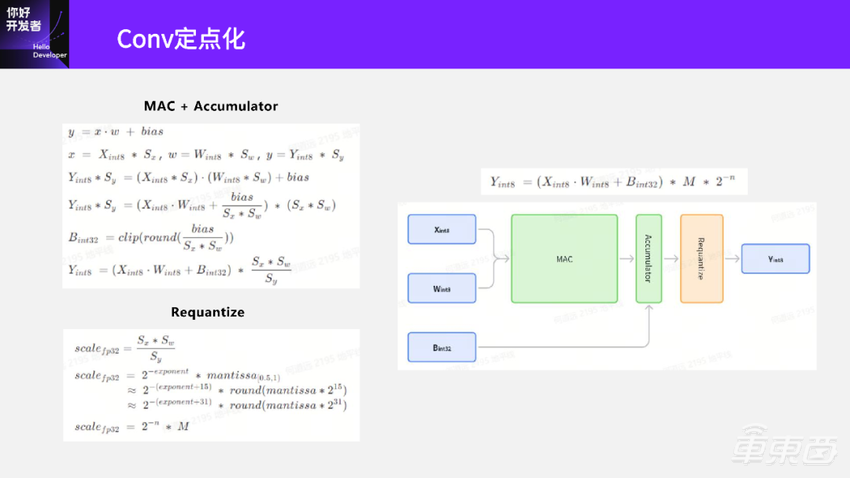
可以看到输入是两个，一个是INT8的激活，另一个是INT8的权重。输入进来之后先送到 MAC里面计算，计算完之后再送到下一个Accumulator累加器里面；图片可以直接送到Accumulator里面进行累加；累加完了之后再送到下一个Requantize模块里面。这个模块实际上就是上面图片的操作，通过Requantize模块，我们就得到了图片整数的INT8的输出。

接下来，我们再看一下激活函数的定点化问题。

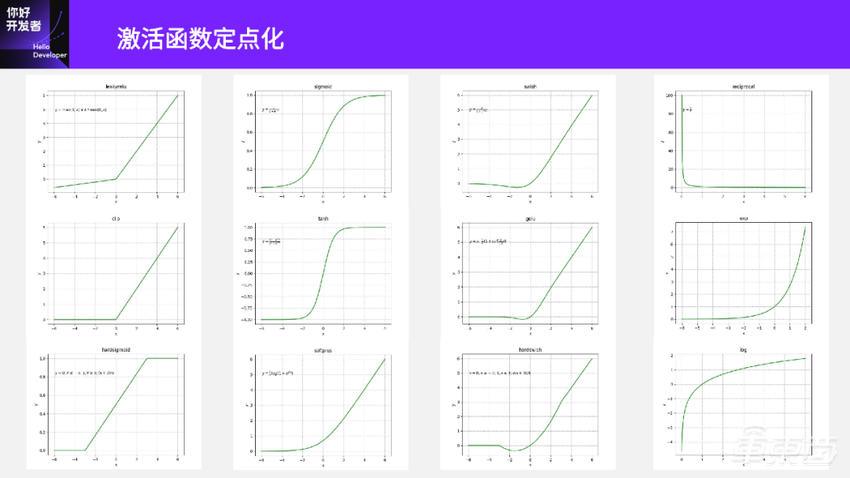
这里列了一些常见的激活函数，实际还有更多。ONNX里面大概有四十几种激活函数。

可以看到这些激活函数差别还挺大的，第一列基本都是一些分段线性的函数，比如最上面的leakyrelu有两段；中间的clip，左边是饱和的；最下面hardsigmoid两端是饱和的，中间是一段线性。

第二列看起来是一些单调递增的函数，比如Sigmoid、Tanh、Softplus都是单调递增。

第三列是CNN里面常用的一些激活函数，比如说这些函数都跟Relu长得比较像，但在靠近0的部分都是一段曲线，而且也各不一样。

第四列是一些下降或上升比较快的函数。第一个是Reciprocal求倒数、第二个是Exp、第三个是Log。

那怎样去实现这些激活函数的计算呢？如果在模型里面遇到了这些激活，怎样实现模型的全整型计算？

第一个办法，我们可以尝试用多项式来拟合这些激活函数。

比如右边这个公式：目标函数是，可以尝试构建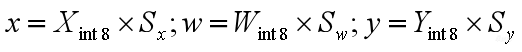这样一个多项式，去拟合f（x）这个目标函数。拟合之后再对多项式进行量化，然后进行定点化，就可以达到全整型计算的目的。

但是多项式拟合也有一些代价。我们看右下角这张图，这是用多项式去拟合Sigmoid的函数：

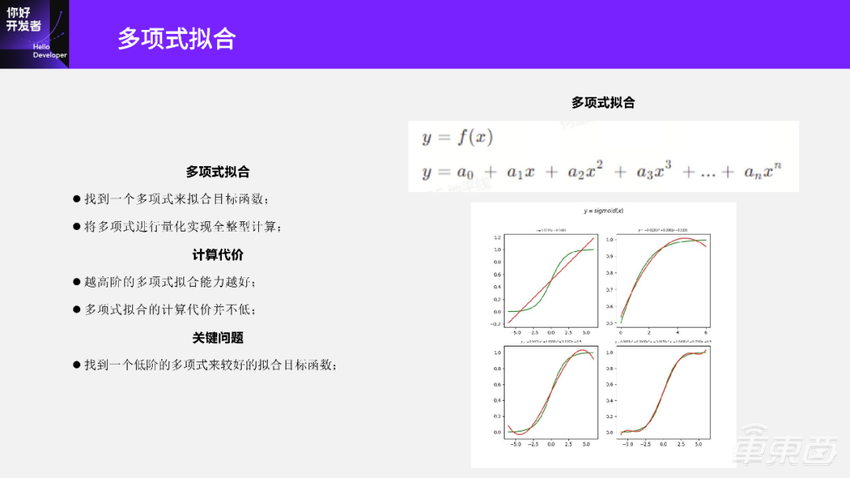
第一个图是一阶的函数，一阶只能拟合线性，拟合不了Sigmoid。

第二个是二阶的函数，它只能拟合一半的Sigmoid。

左下角是一个三阶函数，它基本快拟合到Sigmoid。

右下角是一个五阶的函数，这个拟合的稍微好一点。

多项式拟合往往是越高阶的拟合越好，但是越高阶的计算代价就越高。

我们先考虑一阶的，比如a0+a1x。浮点上需要一次乘法和一次加法，如果我要把浮点的a0+a1x转换成定点的，需要用到前面讲到的Conv定点化中的Requantize那部分的逻辑，先把a0提出来，再把括号里面的a1/a0浮点数拆解成，这样括号里面是一次乘法、一次移位和一次加法操作，括号外面的a0也需要拆分成形式，又需要一次乘法和一次移位操作。

如果考虑多阶的，比如五阶的X^5，大家可以算一下大概需要多少次的乘加以及移位操作，才能完成计算。这个计算代价实际上是不低的。

另外，如果用高阶多项式去拟合还会有溢出风险。可以考虑一下，假设x输入范围是INT8的数据，如果是一个五阶的的操作，数据范围大概是多少呢？实际上已经溢出INT32的范围了，相当于如果用五阶多项式去拟合目标函数，即使输入INT8，也需要用超过INT32的计算能力来计算，这样它的计算代价就更高了。

所以，多项式拟合里面一个关键问题，是能不能找到一个低阶的函数来拟合目标函数。

但一阶就不用想了，它只能拟合线性的。可以考虑二阶的函数，它可以比较好的拟合目标函数或目标函数的一部分。如果能够找到，我们就可以尝试用多项式拟合去做。

我们再介绍另外一种计算代价小的查表计算方法：

1、INT8查表

首先看一下，当输入数据是INT8时候的查表计算方法。

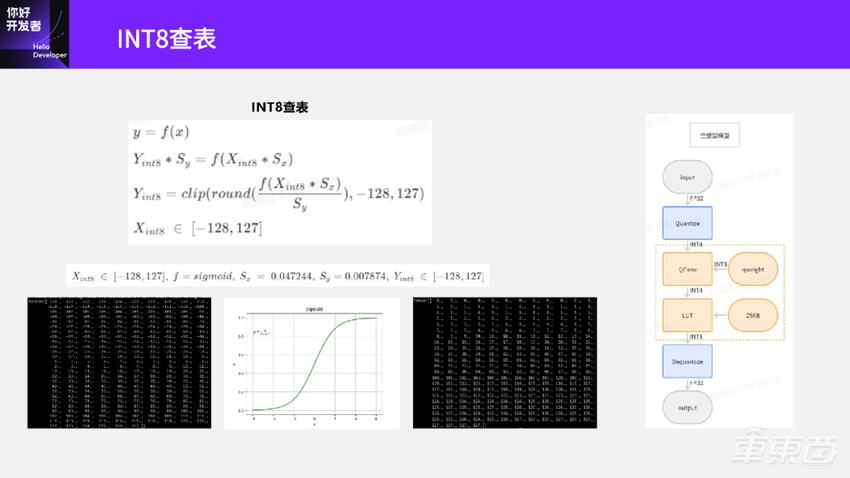
先看一下目标函数y=f(x)，假设为，经过PTQ阶段，我们已经得到 x和 y的量化参数Sy和Sx，带到目标函数里面就有了量化计算公式。

把Sy移过来，把量化函数做一下变换，就得到了第三个式子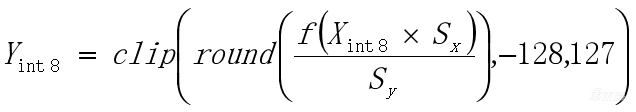。括号里面先取一次round，把这个数整数化，再做一次clip，如果Y是INT8输出的，那么clip的范围是-128~127。

其中函数f是常量，在模型里面肯定知道激活函数是什么，Sy和Sx也是常量，在PTQ阶段已经算出来了。Xint8虽然是个变量，但是它的范围是-128~127。已知Xint8在-128~127范围，假设目标函数是Sigmoid，且PTQ经算出了输入、输出的Sx=0.047244，Sy=0.00787。我们怎么做呢？我们可以尝试遍历所有Xint8从-128~127的值，代入到上面这这个式子里面算一下，得到了每一个Xint8输入情况对应Yint8输出的结果，就是右边这个表。

得到这个表之后，把这个表作为 LUT算子的参数。在推理的时候，先将这个表加载起来，QConv算出INT8数之后，在这个表里面查一下对应的输出是什么，这样就相当于我只要做一次查表操作就得到结果。这种方法在实际推理的时候，只需要预先加载一个256字节的表，在推理的时候，只要需要在表里查一下数据就可以得到结果，比直接计算要更快一些了。

2、INT16查表

我们前面讲到激活量化的时候提到了Layerwise量化参数搜索，对于有一些量化比较敏感的层会尝试用更高Bit量化，比如用INT16去量化。当遇到激活函数输入是INT16时候该怎么做呢？
看一下左边这张图，假设QConv输出INT16的时候激活函数怎么做？

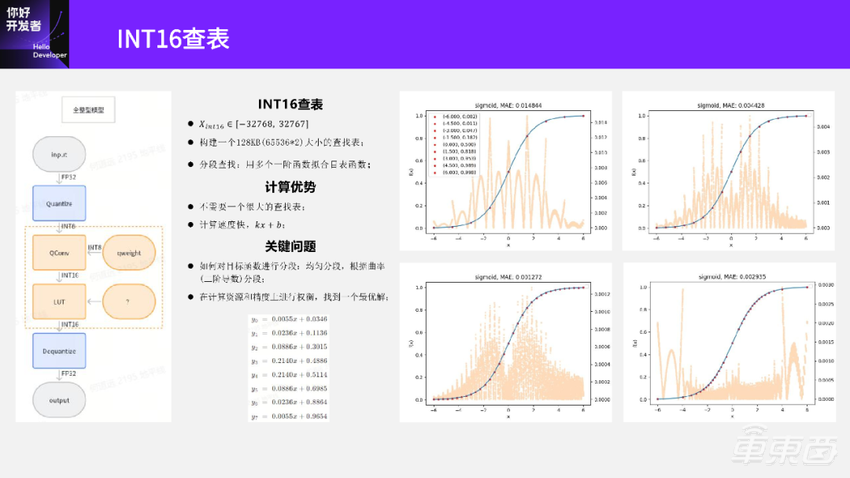
我们前面讲浮点Conv到定点Conv转换的时候，只讲了怎么输出一个INT8的Conv，实际上也可以输出INT16的Conv，并不是那么复杂，大家可以回到前面那页PPT自己推理一下。假设前面这一层Conv输出的是INT16，这时候激活该怎么做呢？如果我们采用Xint8一样的方式会存在一个问题。Xint16的取值范围比Xint8大得多，在-32768~32767之间，如果和Xint8一样就需要构建一个128KB大小的查找表来做。

但128KB就比较夸张了。前面QConv这一层量化后的权重本身可能就没有128KB这么大，如果激活表这么大显然不是很合理。另外，如果真的构建这样一个表并尝试在硬件上用查找的方式去做，计算代价也会是很高的。实际中也不会有人真正去构建这样的表用于推理的时候计算。

那要怎么做呢？这里介绍一个分段查找的方法。

分段查找实际上也是一种目标函数的拟合方法，跟前面讲的多项式拟合方法的差别是：

多项式拟合是用一个多项式去拟合目标函数，而分段查找是用多个一阶函数去拟合目标函数。

右边的图是Sigmoid分段的方法。分段拟合就是先把目标函数分成很多个段。比如第一个图把 Sigmoid用9个点分成8个段，每段用一个一阶函数kx+b去拟合，用这样的方式代替整个目标函数的计算。大家可以很容易想到，分段拟合分的越细，误差肯定越小。蓝色的是Sigmoid曲线；红点就是分段的点；背景上这些橙色的点是误差，它表示的意义是在这个数值附近，用一阶的线性函数kx+b和原始函数算得的结果误差大小。

可以看到，如果分成8个段去拟合，它的最大误差（MAE）在0.014左右。看第二个图，如果用16个段去拟合，那么它的误差就减少了，变成了0.0044。如果是第三个图，用更多的32段去拟合，它的最大误差MAE已经降到了0.0012。

分段查表方法的好处是：我们不需要一个很大的查找表，计算速度也比较快，因为在每一个点上只需要计算一次kx+b就够了。

分段查表有两个问题：一个是怎么对函数进行分段，另一个是分段的个数。

前面三个图都是均匀分段，比如第一个分成8段，就在目标函数范围里平均分成8段；左下角这张图是分成32段，也是在目标函数范围里平均分成32段。

再看一下右下角这张图。很明显这张图的分段就不是均匀的了，那这些图上的点是怎么分的呢？我们是根据曲率或者目标函数的二阶导数去分，曲率代表的是曲线的弯曲程度，曲率越大越弯曲。为什么要用曲率去划分呢？因为如果这个地方弯曲程度比较大，用一段线性去拟合的误差可能会更大。所以一般我们在曲率比较大的地方分的比较密，在曲率比较小的地方就分的比较稀疏，这样就得到了最右边这张图。

我们可以对比一下左下角和右下角这两张图。它们都是对目标函数进行32个分段的，橙色的点是每一个数值上的误差，可以看到左下角这图在0附近，特别是-2~2附近，它的误差是比较大的。右下角这个图在-2~2附近，它的误差明显比较小，误差在两端比较大。因为两端只有一段，没有像左下角那个图一样分的比较密，所以两端的误差比较大。

这是一个权衡问题，激活函数到底哪一部分数据的误差对模型影响比较大？如果中间这部分的误差对整个模型精度比较大，那可以尝试用曲率的方法进行分段；如果两端误差影响比较大，那么你也可以进行均匀分段。

实际上，除了这两种方法还可以任意分段，根据真实的数据分布尝试用不同的方法去做分段，可以得到不同的效果。

另外就是分段的个数，分的越密误差越小，分的越稀疏误差就会越大。

最后再看一下，分完段之后我们应该怎么做。还以左上角这个图为例，将Sigmoid 分成了8个段之后，我们就可以得到每一段的线性拟合函数。可以看到左下角 y0=0.0055x+0.0346，y1、y2等，一直到y7，一共有8个式子。这8个式子还是浮点的，还是需要把它们定点化（整数化）。实际上和前面提到的Requantize那部分逻辑类似，把浮点数提出来转换成整数乘法和移位操作，就可以把这些计算公式整数化。

整数化之后，我们就可以得到8个公式。这8个公式我们就加载到最左边这个图的LUT算子里面。作为它的常数，在模型推理的时候，先把LUT的8个式子都加起来，当有数据进来的时候，判断这个数据是落在哪一段，就用哪一段公式去计算，算完之后输出相应的结果。

这种方式加载的常数表远远不需要128KB大小，而且计算速度比较快，因为对于每一个数据都是一次kx+b线性计算。不过，在最终硬件上还是需要去权衡到底分成多少个段，用怎么样的方法来保证硬件代价是最小的，并且精度是有保障的。

我今天的分享到这里就结束了，谢谢大家。